OpenWAM » Scientific documentation » Open end boundary

Open end boundary

By | | Scientific documentation

Contents

Physical phenomenon for open end

Phenomenon that takes place at the end of a pipe mainly depends on flow direction, so that it is necessary to determine it previously. In order to do this, it is assumed in stationary conditions (the pressure at pipe’s end and the exterior pressure are the same). It is possible to express pressure by means of characteristics variables; that is:

(1)   \begin{equation*} p = p_{ref} \left( {\frac{A}{{A_A }}} \right)^{\frac{{2\gamma }}{{\gamma - 1}}} \end{equation*}

Where A_A is the entropy level and A dimensionless speed of sound, that is related with
characteristics variables.

(2)   \begin{equation*} p_a < \left( {\frac{{\lambda _{in,1} + \lambda _{out,1} }}{{2A_{A_1 } }}} \right)^{\frac{{2\gamma }}{{\gamma - 1}}} p_{ref} \end{equation*}

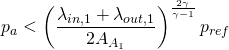
Working out the value for pressure:

(3)   \begin{equation*} \left( {\frac{{p_a }}{{p_{ref} }}} \right)^{\frac{{\gamma - 1}}{{2\gamma }}} < \frac{{\lambda _{in,1} + \lambda _{out,1} }}{{2A_{A_1 } }} \end{equation*}

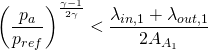
Due to flow is going out the pipe it is certain that:

(4)   \begin{equation*} \left| {U_1 } \right| = \frac{{\lambda _{in,1} - \lambda _{out,1} }}{{\gamma - 1}} \to \left| {U_1 } \right| > 0 \to \lambda _{in,1} > \lambda _{out,1} \end{equation*}

Taking into account the inequality in characteristic values, it is possible to present the next equation:

(5)   \begin{equation*} \frac{{\lambda _{in,1} + \lambda _{out,1} }}{{2A_{A_1 } }} < \frac{{2\lambda _{in,1} }}{{2A_{A_1 } }} = \frac{{\lambda _{in,1} }}{{A_{A_1 } }} \end{equation*}

Due to flow is going out the pipe it is certain that:

(6)   \begin{equation*} \left| {U_1 } \right| = \frac{{\lambda _{in,1} - \lambda _{out,1} }}{{\gamma - 1}} \to \left| {U_1 } \right| > 0 \to \lambda _{in,1} > \lambda _{out,1} \end{equation*}

Taking into account the inequality in characteristic values, it is possible to present the next equation:

(7)   \begin{equation*} \frac{{\lambda _{in,1} + \lambda _{out,1} }}{{2A_{A_1 } }} < \frac{{2\lambda _{in,1} }}{{2A_{A_1 } }} = \frac{{\lambda _{in,1} }}{{A_{A_1 } }} \end{equation*}

Then

(8)   \begin{equation*} \left(\frac{p_a}{p_{ref}}\right)^{\frac{\gamma-1}{2\gamma}}<\frac{\lambda_{in}}{A_{A1}}=\frac{\hat \lambda_{in}}{\hat A_A} \end{equation*}

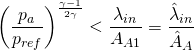
In conclusion:

  • Outgoing flow:

        \[\frac{\hat\lambda_{in}}{\hat A_A}>\left[\frac{p_a}{p_{ref}}\right]^{\frac{\gamma-1}{2\gamma}}\]

    Similarly to outgoing flow, next cases are obtained and showed in the equations below.

  • Stationary flow

        \[\frac{\hat\lambda_{in}}{\hat A_A}=\left[\frac{p_a}{p_{ref}}\right]^{\frac{\gamma-1}{2\gamma}}\]

  • Flow going into

        \[\frac{\hat\lambda_{in}}{\hat A_A}<\left[\frac{p_a}{p_{ref}}\right]^{\frac{\gamma-1}{2\gamma}}\]

Phisical model for open end boundary

Due to physical phenomenon depends on flow direction; the employed model will also depend on it. In the next paragraphs are presented the necessary hypothesis for outgoing flow and ingoing flow.

Flow going out

Subsonic flow

When flow is going out the pipe, it can be considered that pressure loss between the last cross sectional area of the pipe and the exterior are not important. So, it is assumed that pressure will be the same; according to this, the working fluid is getting laminar at constant pressure up till it loses its velocity by friction with surrounding air.
Owing to \lambda_{in} and A_A are known in this situation, it is only necessary to determine the \lambda_{out} value. Remembering that pressure at the end of pipe has been supposed the same as the exterior one, we have:

(9)   \begin{equation*} p_a=p=p_{ref}\left[ \frac{A}{A_A} \right]^{\frac{2\gamma}{\gamma-1}} \end{equation*}

Where working out the speed of sound A , and replacing it in the definition of characteristic variables, it is obtained finally:

(10)   \begin{equation*} \lambda_{out}=2A_A\left[\frac{p_a}{p_{ref}} \right]^{\frac{\gamma-1}{2\gamma}}-\lambda_{in} \end{equation*}

Supersonic Flow

At supersonic situation, A<\left|U\right| ,it is simply imposed that flow velocity at the outgoing section is equal to the speed of sound A=\left|U\right| (sonic condition).The condition of sonic limit A=\left|U\right| leads to:

(11)   \begin{equation*} \lambda_{out}=\frac{3-\gamma}{\gamma+1}\lambda_{in} \end{equation*}

Flow going into

Subsonic flow

In general situation pressure losses are produced and the streamline suffers a contraction that implies a reduction in flow velocity and so a reduction in the ingoing mass flow. These losses are taken into account by means of a velocity loss coefficient.
In this case the energy equation is presented between the final section and the exterior:

(12)   \begin{equation*} A^2+\frac{\gamma-1}{2}\left|U\right|^2=A^2_a \end{equation*}

The incident characteristic equation for ingoing flow is:

(13)   \begin{equation*} A\frac{\hat A_A}{A_A}=\hat \lambda_{in}+\frac{\gamma-1}{2}\left|U\right| \end{equation*}

And the loss velocity coefficient is:

(14)   \begin{equation*} \psi=\frac{\left|U \right|}{\left|U_s\right|} \end{equation*}

Where \left|U_s\right| is the highest speed and it corresponds to the isentropic case and \psi has to be obtained experimentally.

The introduction of the auxiliary variable |U_s| requires additional equations that correspond to suppose an isentropic evolution between the exterior and pipe:

(15)   \begin{equation*} A^2_s+\frac{\gamma-1}{2}\left|U_s\right|^2=A^2_a \end{equation*}

(16)   \begin{equation*} A_{As}=A_{Aa} \end{equation*}

(17)   \begin{equation*} \frac{A}{A_A}=\frac{A_s}{A_{As}} \end{equation*}

Where working out \left|U_s\right| is obtained the value of \left|U\right| is obtained the value of \left|U\right|=\psi\left|U_s\right|

And the isentropic speed of sound:

    \[A_s=\sqrt{A_a^2-\frac{\gamma-1}{2}\left|U\right|^2}\]

Once \left|U\right| and A_a are known, A is obtained from energy equation:

    \[A=\sqrt{A_a^2-\frac{\gamma-1}{2}\left|U\right|^2}\]

And value for entropy level will be obtained from:

    \[A_A=A\frac{A_A_a}{A_s}\]

Finally the known characteristic \lambda_{in} is calculated directly using A and \left|U\right|
values:

    \[\lambda_{in}=A-\frac{\gamma-1}{2}\left|U\right|\]

Supersonic Flow

In this situation it is supposed that working fluid suffers an expansion with such losses that final conditions are always sonic.

If sonic conditions are forced is not necessary to introduce pressure loss coefficient, so only are planted the incident characteristic equation and energy equation, besides sonic condition.

    \[A=\left|U\right|\]

In this case sound velocity A is directly obtained from energy equation:

    \[A=\sqrt{\frac{2}{\gamma+1}}A_a\]

And value for entropy level is obtained from incident characteristic equation:

    \[A_A=\frac{\hat A_A \cdot A}{\hat \lambda_{in}-\frac{\gamma-1}{2}\left|U\right|}=\frac{\hat A_A \cdot A}{\hat \lambda_{in}-\frac{\gamma-1}{2}A}\]

Finally known characteristic \lambda_{in} is calculated in the same manner than subsonic flow.

    \[\lambda_{in}=A-\frac{\gamma-1}{2}\left|U\right|\]

Bookmark the permalink.

Comments are closed.